Four Triangles and Three squares

The picture here holds something really cool:

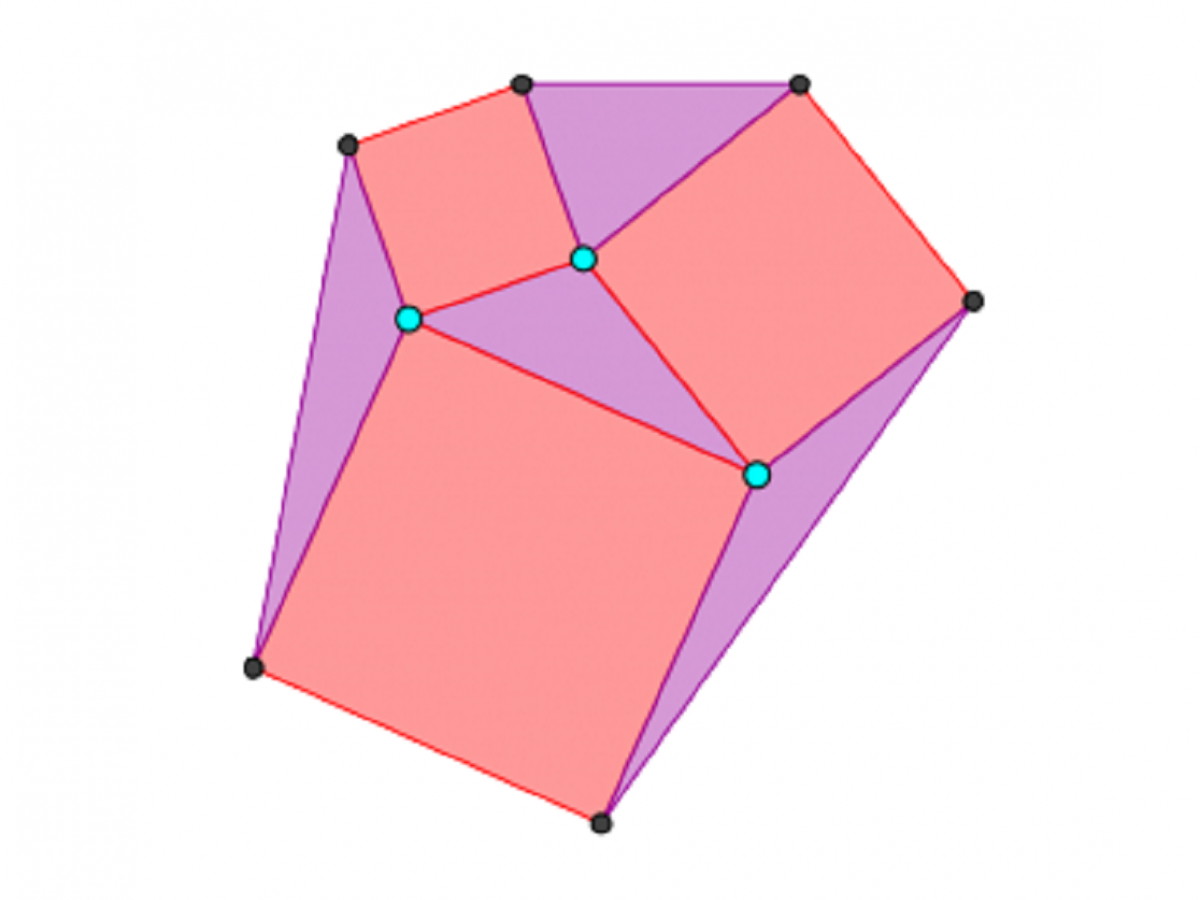
To make a picture like this, you begin with a triangle, then you construct a square on each side (like with Pythagoras' Theorem). After that, you join the corners of the squares together to produce three more triangles. So in the end you have four triangles – which I've coloured in purple in the picture – and three squares – which I've coloured red.

When you construct the picture in this way then the following is true: the four triangles each have the same area!

Isn't that cool?!

The thing that makes it even cooler is why the four triangles all have the same area. If you rotate one of the side triangles until its edge meets the middle triangle, you'll make one bigger triangle. The two triangles have the same base length and their top points are in the same place, so they also have the same height. So they must have the same area, since the area of a triangle is determined by the length of its base and the height of the point above the base.

Again I say: isn't that cool?